模型详解配置
2025/7/9...大约 4 分钟
模型详解配置
构建大模型需要考虑的因素归一化方法、位置编码、激活函数、注意力计算
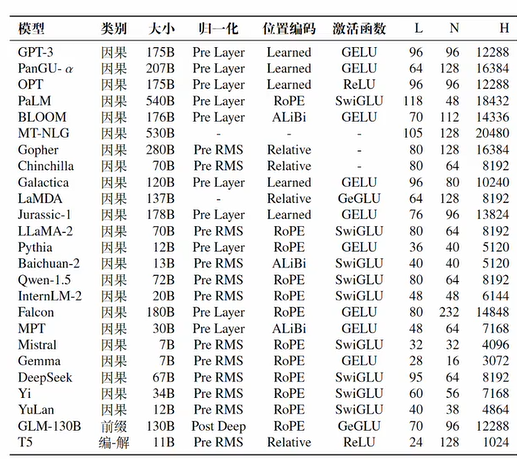
层数L、注意力头数N、特征维度N
归一化方法
为什么要做归一化?
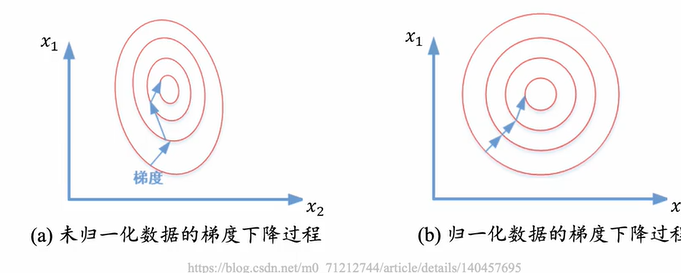
不同特征在空间中的尺度不同,对损失优化的影响不一致
特征尺度差异会导致损失函数各方向的梯度下降速度不同。尺度大的特征梯度更新剧烈,迫使模型花费更多迭代次数调整其他特征权重,降低优化效率。提升训练稳定性,加速模型收敛
归一化使所有特征处于相近的数值范围(如[0,1]或[-1,1])。这使优化路径更平滑,梯度更新方向更稳定,减少震荡风险,从而加快模型收敛速度。
方法

归一化模块位置
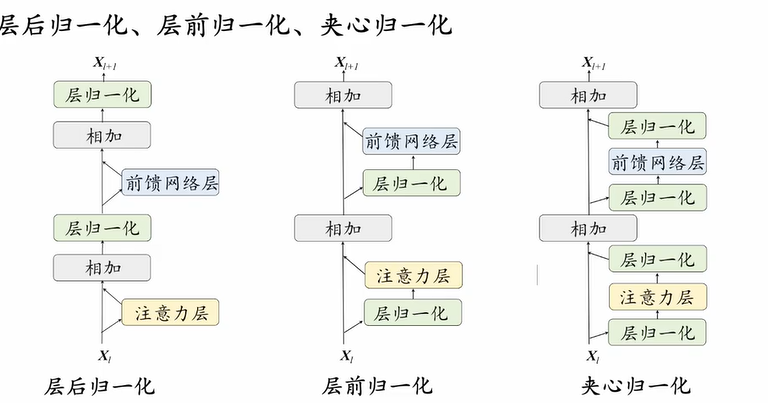
层后归一化(Post-Layer Normalization, Post-Norm)
定义 (归一化模块放置于残差计算之后)
优点
- 加快训练收敛速度
- 防止梯度爆炸或梯度消失
- 降低神经网络对于超参数的敏感性
缺点
- 可能导致训练不稳定
- 目前较少单独使用
层前归一化(Pre-Layer Normalization, Pre-Norm)
定义 (归一化模块应用在每个子层之前)
优点
- 训练更加稳定
- 主流模型采用较多
缺点
- 性能略有逊色
夹心归一化(Sandwich-Norm)
定义 (通过双重归一化叠加:在子层前和子层后各加一次归一化)
核心特性
- Pre-Norm与Post-Norm的复合结构
- 归一化逻辑:输入 → 首次归一化 → Sublayer计算 → 二次归一化 → 残差连接
优势
- 理论上融合Pre-Norm的稳定性与Post-Norm的性能增益
- 梯度调节能力更强(双重归一化约束)
局限性
- 计算开销显著增加(额外归一化层)
- 仍存在训练震荡风险
- 实际应用较少,多见于理论研究
位置编码

绝对位置编码代表性的是旋转位置编码
绝对位置编码:旋转位置编码

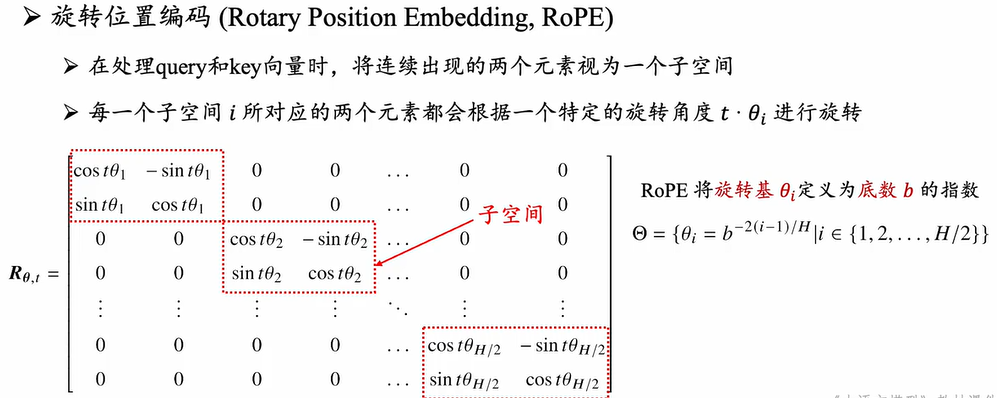
相对位置编码:ALiBi位置编码

激活函数

注意力计算
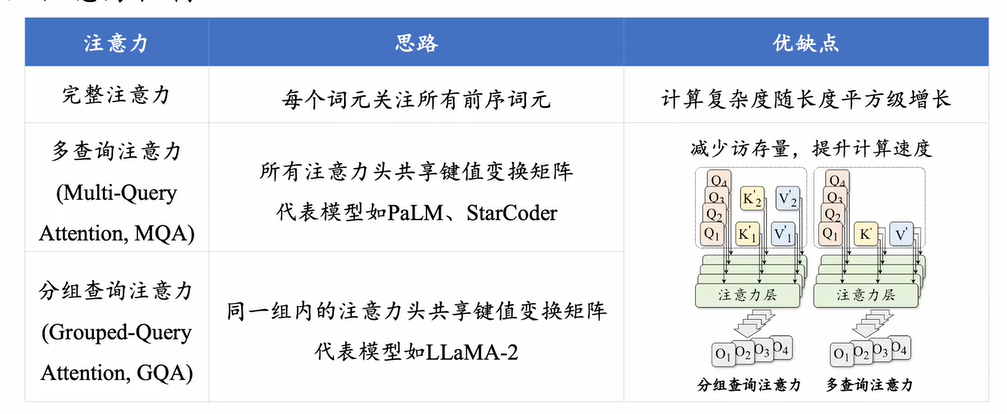
对硬件优化
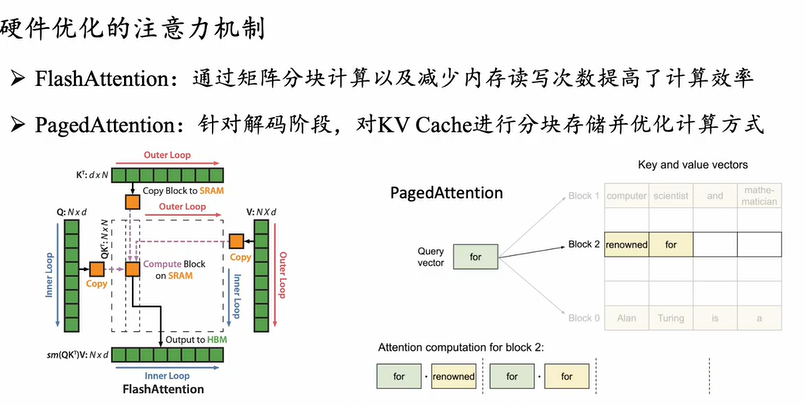
MOE模型
举例: deepseek、Mixtral
目的是在不显著提升计算成本的同时实现对于模型参数的扩展。
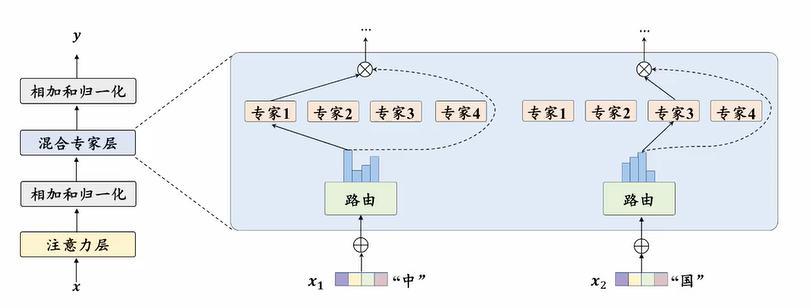
混合专家架构(Mixture-of-Experts, MoE)
核心定义
$$ \text{MoELayer}(x_t) = \sum_{i=1}^{K} G(x_t)_i \cdot E_i(x_t)
$$ 其中路由函数:
$$ G(x_t) = \text{softmax}(\text{topk}(x_t \cdot W_G))
$$
基本组成
专家组件
- $K$个独立的前馈神经网络 ${E_1, E_2, ..., E_K}$
- 每个专家具备相同网络结构,参数不同
路由网络
- $W_G$:权重矩阵(将输入词元$x_t$映射为$K$维得分向量)
- $\text{topk}$:选择得分最高的$k$个专家(通常$k \ll K$)
- $\text{softmax}$:归一化获得激活权重(未选中专家权重置$0$)
运行流程输入词元 → 路由计算→ 筛选topk专家→ 专家并行计算→ 加权输出求和
核心优势
- 稀疏激活:仅计算部分专家输出(节省计算资源)
- 超参扩容:通过增加专家数$K$提升模型容量(计算量仅由$k$决定)
- 动态适配:根据输入特性自动分配处理专家
显著局限
- 路由决策不可导(需直通估计器技巧)
- 专家负载不均衡风险(需引入辅助损失)
- 通信开销大(分布式训练时专家间数据交换)
常用
| 模型 | 混合专家 | 归一化 | 位置编码 | 激活函数 | 注意力机制 | 层数 | 隐藏层维度 | 注意力头个数 | 头维度 |
|---|---|---|---|---|---|---|---|---|---|
| LLaMA-3.1 (405B) | N/A | Pre RMSNorm | 旋转位置编码 | SwiGLU | 多头隐式注意力 | 126 | 16,384 | 128 | 128 |
| DeepSeek (67B) | N/A | Pre RMSNorm | 旋转位置编码 | SwiGLU | 多头隐式注意力 | 95 | 8,192 | 64 | 128 |
| DeepSeek-V2 (236B) | 162 Experts | Pre RMSNorm | 旋转位置编码 | SwiGLU | 分组查询注意力 | 60 | 5,120 | 40 | 128 |
| DeepSeek-V3 (671B) | 257 Experts | Pre RMSNorm | 旋转位置编码 | SwiGLU | 分组查询注意力 | 61 | 7,168 | 56 | 128 |
更新日志
2025/7/9 09:56
查看所有更新日志
171b9-于